Final answer:
To find the critical values for a 95% confidence interval of the sample mean cost of automobile repairs, use the Z-table or software with a Z-score of approximately ±1.96, multiplying by the standard error of the mean (SEM).
Step-by-step explanation:
To find the critical values for a normally distributed variable, you typically refer to the Z-table or use statistical software. The critical values correspond to the Z-scores that define the tails of the distribution, indicating the range within which a certain percentage of the data falls.
Since the standard deviation of the sample costs is given as $120.82, you'll need to use this information to calculate the standard error of the mean (SEM), which is given by the formula:
![\[SEM = (s)/(√(n))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/d884f3f6xo5z4ovsug5jz579h4jwb0iesr.png)
where
 is the sample standard deviation and
is the sample standard deviation and
 is the sample size. In this case,
is the sample size. In this case,
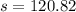 and
and
 .
.
![\[SEM = (120.82)/(√(15))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/v4y3kua52zj8ow3z95c9owbwjhjkp136wd.png)
After calculating the SEM, you can use it to find the critical values based on the desired level of confidence (usually 90%, 95%, or 99%). The critical values correspond to the Z-scores that cut off the tails of the normal distribution.
For example, if you want to find the critical values for a 95% confidence interval, you'll look for the Z-scores that leave 2.5% in each tail. You can then use these Z-scores to find the corresponding raw values by multiplying them by the SEM and adding/subtracting from the sample mean.