Question

(2x ^ 2 + 6x - 6)/(x ^ 3 - 1)Write each of the following rational expressions as a sum of partial fractions.

Answer 1

To write the given rational expression as a sum of partial fractions, first factor the denominator. Then set up an equation with unknown fractions A, B, and C. Solve the equation to find the values of A, B, and C, and substitute them back into the equation to express the rational expression as a sum of partial fractions.

To write the rational expression as a sum of partial fractions, we first factor the denominator,
`x^3 - 1.`The denominator can be factored as (x - 1)
`(x^2 + x + 1).` Since the denominator has a degree of 3, we will have three partial fractions. Let's call the three fractions A, B, and C. We can set up the equation as:

`(2x^2 + 6x - 6)/(x^3 - 1) = A/(x - 1) + (Bx + C)/(x^2 + x + 1)`

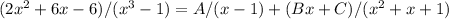
To find the values of A, B, and C, we can clear the fractions by multiplying both sides of the equation by the denominator:

`(2x^2 + 6x - 6) = A(x^2 + x + 1) + (Bx + C)(x - 1)`

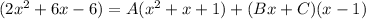
Now we can expand and collect like terms:

`2x^2 + 6x - 6 = Ax^2 + Ax + A + Bx^2 + Cx - Bx - C`

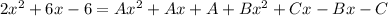
Matching the coefficients o
`f x^2, x,` and the constant term on both sides of the equation, we get:

A + B = 2, A - B + C = 6, A - C = -6

Solving this system of equations will give us the values of A, B, and C, which we can substitute back into the equation to write the rational expression as a sum of partial fractions.