Question

Binomial Probability Really Big Medical Center (RBMC) is testing patients who have spent time in grassy areas this summer and fall for Lyme disease. Suppose that the probability of someone with exposure to tall grass having Lyme is .3 (or 30 percent). In a sample of 15 patients, what is the standard deviation of the number of patients with Lyme disease?

Answer 1

The standard deviation of the number of patients with Lyme disease in a sample of 15, with a probability of 0.3, is approximately 1.7748 patients.

Step-by-step explanation:

The question involves calculating the standard deviation of a binomial distribution. In this case, the data represents the number of patients with Lyme disease out of a sample of 15 patients, where each patient having Lyme disease is considered a 'success'. The probability of 'success' is given as 0.3 (or 30%).

To find the standard deviation of the binomial distribution, we use the formula
`\( \sigma = √(n \cdot p \cdot q) \)`, where
`\( \sigma \)` is the standard deviation ,
`\( n \)` is the number of trials (in this case, 15 patients),
`\( p \)` is the probability of success (0.3), and
`\( q \)` is the probability of failure which is
`\( 1 - p \) (0.7).`

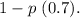
Calculating the standard deviation:

• First find the value of
  `\( q \)` , which is
  `\( 1 - 0.3 = 0.7 \).`
• Now apply the formula:
  `\( \sigma = √(15 \cdot 0.3 \cdot 0.7) \).`
• 
  `\( \sigma = √(3.15) \).`
• 
  `\( \sigma \approx 1.7748 \).`

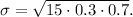
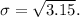
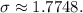
The standard deviation of the number of patients with Lyme disease is approximately 1.7748 patients.