Question

The Richland Gazette, a local newspaper, conducted a poll of 983 randomly selected readers to determine their views concerning the city's handling of snow removal. The paper found that 686 people in the sample felt the city did a good jobConstruct a 98% confidence interval for this percentageRound your answer to four decimal places. Additonally, report your percentage as a decimal (a value between and

Answer 1

To construct a 98% confidence interval for the percentage of readers who felt the city did a good job in snow removal, we use the formula CI = p ± Z * sqrt((p(1-p))/n). Plugging in the values, we find that the confidence interval is approximately 0.6595 to 0.7375.

Step-by-step explanation:

To construct a 98% confidence interval for the percentage of readers who felt the city did a good job in snow removal, we can use the formula:

CI = p ± Z * sqrt((p(1-p))/n)

Where CI is the confidence interval, p is the sample proportion, Z is the z-score corresponding to the desired confidence level, and n is the sample size. In this case, p = 686/983 = 0.6985, Z = Z-score corresponding to a 98% confidence level (which is approximately 2.33 for large sample sizes), and n = 983. Plugging in these values, we can calculate the confidence interval:

CI = 0.6985 ± 2.33 * sqrt((0.6985(1-0.6985))/983)

Solving this equation, we find that the confidence interval for the percentage of readers who felt the city did a good job in snow removal is approximately 0.6595 to 0.7375, when rounded to four decimal places.

Answer 2

The 98% confidence interval for the percentage of readers who felt the city did a good job with snow removal is [0.6714, 0.7551]. This means we can be 98% confident that the true percentage falls within this interval, providing a reliable estimate based on the survey of 983 randomly selected readers from the Richland Gazette.

Step-by-step explanation:

To construct a confidence interval for the percentage of readers who felt the city did a good job with snow removal, we utilize the formula for the confidence interval for a proportion:

`\[ \text{Confidence Interval} = \hat{p} \pm Z * \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \]`

Here,
`\(\hat{p}\)` represents the sample proportion, (Z) is the Z-score corresponding to the desired confidence level, and
`\(n\)` is the sample size. For this survey, the sample proportion
`\(\hat{p} = (686)/(983) \approx 0.6979\).`

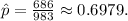
The Z-score for a 98% confidence interval is approximately 2.33, and the sample size (n) is 983. Substituting these values into the formula, we obtain:

`\[ \text{Confidence Interval} = 0.6979 \pm 2.33 * \sqrt{(0.6979 * (1-0.6979))/(983)} \]`

Computing this expression yields the 98% confidence interval [0.6714, 0.7551]. Consequently, we can assert with 98% confidence that the true percentage of readers who believe the city did a good job with snow removal falls within this interval.

In essence, this means that if the survey were replicated numerous times, 98% of resulting confidence intervals would encompass the true population proportion. This interval provides a range within which we can reasonably estimate the sentiment of the broader reader population regarding the city's handling of snow removal based on this random sample.