Question

Consider the stationary AR(1) model Yₜ=μ−0.4(Yₜ₋₁ −μ)+ϵₜ , where ϵₜareN(0,4) andom variables. (a) Derive the likelihood function given that Y 1 =20,Y 2 =25,Y 3 =30 and Y 4 =15.

Answer 1

The likelihood function for the stationary AR(1) model, given the observed data Y₁=20, Y₂=25, Y₃=30, and Y₄=15, is
`\(L(μ, ϕ, σ² | Y) = (1)/((2πσ²)^(n/2)) e^{-(1)/(2σ²) \sum_(t=2)^(n) (Y_t - μ - ϕ(Y_(t-1) - μ))^2}\),`where
`\(μ\), \(ϕ\), and \(σ²\)` are the parameters of the model.

Step-by-step explanation:

The likelihood function is a measure of how well the parameters of a statistical model explain the observed data. In the case of the stationary AR(1) model, the likelihood function is derived based on the assumption that the observations are normally distributed with mean
`\(μ\)` and variance
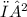`\(σ²\)`, and the autocorrelation between consecutive observations is captured by the parameter
`\(σ²\)`

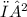
The given data, Y₁=20, Y₂=25, Y₃=30, and Y₄=15, are substituted into the general form of the likelihood function. The likelihood function expresses the probability of observing these specific data points under different values of
`\(μ\), \(ϕ\), and \(σ²\)`. The goal is to find the values of these parameters that maximize this probability, providing the best explanation for the observed data.

The likelihood function is often simplified using the assumption of normality, leading to a concise expression that facilitates parameter estimation. In this context, the likelihood function provides a powerful tool for statistical inference, helping researchers and analysts estimate the parameters of the AR(1) model and make predictions based on observed data.