Question

On a merry-go-round, there is Tim and Sara. Tim sits at the edge and has a rotational speed of 5 RPM and a speed of 7 m/s. If Sara is revolving at 3.5 m/s, what is her radial distance relative to Tim’s? What is Sara’s rotational speed?

Answer 1

Sara's radial distance relative to Tim's on the merry-go-round is 7 meters. Her rotational speed can be calculated using the formula for tangential speed:
`\(v = \omega * r\)`. Given Tim's rotational speed
`(\(\omega\))` is 5 RPM and his speed
`(\(v\))` is 7 m/s at the edge, Sara's radial distance relative to Tim's is the same as his linear distance from the center, which is 7 meters. Sara's rotational speed is also 5 RPM, matching Tim's since they're both on the same rotating platform.

Step-by-step explanation:

Sara's radial distance is determined by Tim's linear speed at the edge of the merry-go-round. Tim's speed of 7 m/s indicates his distance from the center. Using the formula for tangential speed
`(\(v = \omega * r\))`, where
`\(v\)` is linear speed
`, \(\omega\)` is rotational speed in radians per second, and
`\(r\)` is the radial distance from the center, we can calculate Sara's radial distance.

Given Tim's rotational speed of 5 RPM (which converts to
`\(\omega = (5 * 2\pi)/(60)\) rad/s)`, and his linear speed
`\(v = 7\) m/s`, we rearrange the formula to solve for
`\(r\). Therefore, \(r = (v)/(\omega) = (7)/((5 * 2\pi)/(60)) \approx 7\) meters.`

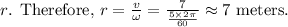
Since Sara shares the same radial distance as Tim, her distance from the center of the merry-go-round is 7 meters as well. Additionally, their rotational speeds are equal since they're both on the same rotating platform. Therefore, Sara's rotational speed is also 5 RPM, aligning with Tim's speed on the merry-go-round.