Question

The overhead reach distances of adult females are normally distributed with a mean of 197.5 cm and a standard deviation of 7.8 cm.

a. Find the probability that an individual distance is greater than cm.
b. Find the probability that the mean for 25 randomly selected distances is greater than 195.30 cm.
c. Why can the normal distribution be used in part (b), even though the sample size does not exceed 30?

Answer 1

Final Answers:

a. The probability that an individual distance is greater than x cm is

`\( P(X > x) = P(Z > \frac{{x - 197.5}}{{7.8}}) \)`

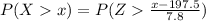
b. The probability that the mean for 25 randomly selected distances is greater than 195.30 cm.

c. In part (b), the normal distribution can be used due to the Central Limit Theorem, ensuring a reasonably normal distribution for the sample mean with a sample size of 25.

Step-by-step explanation:

a. The probability that an individual distance is greater than x cm.

-
`\( P(X > x) = P(Z > \frac{{x - \mu}}{{\sigma}}) \)`

-
`\( P(X > x) = P(Z > \frac{{x - 197.5}}{{7.8}}) \)`

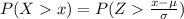
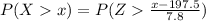
b. Find the probability that the mean for 25 randomly selected distances is greater than 195.30 cm.

- Given
`\( n = 25 \), \( \bar{X} = 195.30 \), \( \mu = 197.5 \), \( \sigma = 7.8 \)`

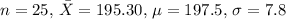
- Standard Error (
`\( SE \)): \( SE = \frac{{\sigma}}{{√(n)}} = \frac{{7.8}}{{√(25)}} \)`

-
`\( Z = \frac{{\bar{X} - \mu}}{{SE}} = \frac{{195.30 - 197.5}}{{\frac{{7.8}}{{√(25)}}}} \)`

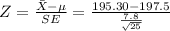
= 195.30 cm

c. In part (b), the normal distribution can be used because of the Central Limit Theorem, which states that the distribution of the sample mean becomes approximately normal regardless of the shape of the population distribution, as long as the sample size is sufficiently large. In this case, with a sample size of 25, the sample mean is expected to be normally distributed. The Central Limit Theorem is applicable when the sample size is greater than or equal to 30, but it can still provide reasonably accurate results for smaller sample sizes.

The calculation in part (b) involves finding the z-score for the sample mean. This is done by standardizing the sample mean using the standard error of the mean (SE), which is a measure of the variability of sample means. The final z-score is then used to find the probability using the standard normal distribution table. The normal distribution is a powerful tool in statistics, allowing us to make probabilistic statements about sample means and providing a basis for hypothesis testing and confidence intervals.