Question

What is the slope of the line that passes through the points (-10,9) and (-10,18) ?

Answer 1

The slope of the line passing through the points (-10,9) and (-10,18) is undefined.

Step-by-step explanation:

To determine the slope of a line using two points, the slope formula
`\( \text{Slope} = \frac{{y_2 - y_1}}{{x_2 - x_1}} \)` is employed. For the given points (-10,9) and (-10,18), the formula is applied:

`\( \text{Slope} = \frac{{18 - 9}}{{-10 - (-10)}} \)`

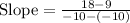
Simplifying the calculation:

`\( \text{Slope} = (9)/(0) \)`

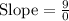
The denominator of zero arises when the x-values of both points are identical. This scenario indicates a vertical line. In geometry, a vertical line's slope is undefined because it doesn't follow the traditional slope pattern of rise over run. Instead, it ascends or descends vertically without a horizontal shift. When x-values are equal but y-values differ, as in this case (-10,9) and (-10,18), it signifies a line that's parallel to the y-axis, hence perfectly vertical. Due to this vertical orientation, the slope is undefined.

Therefore, the line passing through the points (-10,9) and (-10,18) is vertical, and as a result, its slope is undefined in the context of traditional slope calculations.