Final Answer:
The volume of the largest circular cylinder that can be inscribed in a circular cone with radius 5 inches and height 8 inches is
 cubic inches.
cubic inches.
Step-by-step explanation:
Let's denote:
-
 as the radius of the cylinder,
as the radius of the cylinder,
-
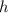 as the height of the cylinder.
as the height of the cylinder.
The cylinder is inscribed in the cone, so its dimensions must satisfy the conditions of the cone. In particular, the radius of the cylinder
 must be equal to the radius of the cone's base (5 inches).
must be equal to the radius of the cone's base (5 inches).
The height of the cylinder
 plus the height of the remaining frustum of the cone must be equal to the height of the cone (8 inches).
plus the height of the remaining frustum of the cone must be equal to the height of the cone (8 inches).
Let's express the height of the frustum
 in terms of
in terms of
 using similar triangles:
using similar triangles:
![\[ (h')/(r) = (8 - h)/(5) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8m43uxs4pwfxdhw5ekpsnxkk8z7yn4mv3b.png)
Solving for
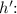
![\[ h' = (r(8 - h))/(5) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5i4nqrrge90bqdkzfie9vjqe9kuqy9q2c3.png)
The volume
 of the cylinder is given by:
of the cylinder is given by:
![\[ V = \pi r^2 h \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ug30de7ei4kh0ajv58c9y4n4ti9utw2few.png)
Substituting the expressions for
 and
and
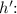
![\[ V = \pi \left(5^2\right) \left((r(8 - h))/(5)\right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vevecwjjws3xx5l46gbdoek6q9mbwt9sau.png)
Simplifying:
![\[ V = (\pi)/(5) r(8 - h)r^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7aropbwpx18a5flyjgvrjhtlu0iq2rlicy.png)
We know that
 (radius of the cone), and
(radius of the cone), and
 (height of the cone). Substituting these values:
(height of the cone). Substituting these values:
![\[ V = (\pi)/(5) \cdot 5(8 - h) \cdot 5^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wrsdwlhm2y5vqexl3auou1gzs3ijg2omhw.png)
Simplifying further:
![\[ V = (320\pi)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/v5844ujlt2yhwxs7kb0309t6fiv9royjpb.png)
Therefore, the volume of the largest circular cylinder that can be inscribed in the given circular cone is
 cubic inches.
cubic inches.