Question

Erify that the function f(x)=e³ satisfies the hypotheses of the Mean Value Theorem on the interval [0, ln 4]. Then find all numbers c that satisfy the conclusion of the Mean Value Theorem.

A. The function does not satisfy the hypotheses of the Mean Value Theorem.
B. The function satisfies the hypotheses, and there is no c that satisfies the conclusion of the Mean Value Theorem.
C. The function satisfies the hypotheses, and c can be any real number in the interval [0, ln 4].
D. The function satisfies the hypotheses, and c can be r³.

Answer 1

The function
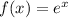`\( f(x) = e^x \)` satisfies the Mean Value Theorem hypotheses on
`\([0, \ln 4]\)`, and
`\( c \)` can be any real number in this interval. This is because the function is continuous and differentiable everywhere, meeting the conditions of the theorem. C. The function satisfies the hypotheses, and c can be any real number in the interval [0, ln 4].

Step-by-step explanation:

The Mean Value Theorem (MVT) states that if a function
`\( f \)` is continuous on the closed interval
`\([a, b]\)` and differentiable on the open interval
`\((a, b)\)`, then there exists at least one number
`\( c \)` in the interval
`\((a, b)\)` such that
`\( f'(c) = (f(b) - f(a))/(b - a) \).`

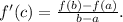
In our case, the function
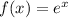`\( f(x) = e^x \)` is continuous and differentiable for all real numbers. Thus, it satisfies the hypotheses of the MVT. The interval
`\([0, \ln 4]\)` is closed and
`\((0, \ln 4)\)` is open, so the conditions are met.

Now, to find
`\( c \)`, we calculate
`\( f' \)`:

`\[ f'(x) = (d)/(dx)(e^x) = e^x \]`

Apply the MVT formula:

`\[ e^c = (e^(\ln 4) - e^0)/(\ln 4 - 0) \]`

Simplify:

`\[ e^c = (4 - 1)/(\ln 4) \]`

Thus,
`\( c \)` can be any real number in the interval
`\([0, \ln 4]\)`, and the correct option is C. The conclusion is that there exists at least one
`\( c \)` in
`\([0, \ln 4]\)`satisfying the MVT for
`\( f(x) = e^x \).`