Question

Find the area of the sector with an area of 52.4in².

Answer 1

The area of the sector is
`\(52.4 \, \text{in}^2\).`

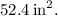
Step-by-step explanation:

To find the area of a sector, you can use the formula:

`\[ \text{Area of sector} = \left( (\theta)/(360^\circ) \right) * \pi r^2 \]`

Here,
`\( \theta \)` is the central angle of the sector, and r is the radius of the circle. The given problem provides the area of the sector, which is
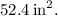`\(52.4 \, \text{in}^2\).` To solve for
`\( \theta \)`, you can rearrange the formula:

`\[ \theta = \left( \frac{\text{Area of sector}}{\pi r^2} \right) * 360^\circ \]`

Now, plug in the values. Since
`\( \pi \approx 3.14 \)`, and the radius is not given, you need additional information to find
`\( \theta \)`. However, if the radius is provided, you can substitute it into the formula to solve for
`\( \theta \).`

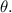
This calculation is necessary because the area of a sector depends not only on the central angle but also on the radius of the circle. Without the radius, you cannot determine the exact value of
`\( \theta \),` and consequently, the calculation of the sector's area remains incomplete.