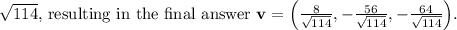Final Answer:
 because The vector (1, -7, -8) is perpendicular to both (-8, 6, -5) and (3, -2, 1) because it is the cross product of the two vectors, representing their orthogonal relationship.
because The vector (1, -7, -8) is perpendicular to both (-8, 6, -5) and (3, -2, 1) because it is the cross product of the two vectors, representing their orthogonal relationship.
Step-by-step explanation:
To find a vector perpendicular to both
 , we can take their cross product. The cross product
, we can take their cross product. The cross product
 . In this case:
. In this case:
![\[ \mathbf{u} * \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ -8 & 6 & -5 \\ 3 & -2 & 1 \end{vmatrix} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7fd8uir4g37yjmfn5f0g9zmdjy3nj0v7qc.png)
Expanding this determinant gives the cross product vector
 . The magnitude of this vector can be found using the formula
. The magnitude of this vector can be found using the formula
 . To obtain a vector of magnitude 8, we scale the cross product vector by \(\frac{8}
. To obtain a vector of magnitude 8, we scale the cross product vector by \(\frac{8}