Question

30 Points! A soccer ball hit from the ground into the air and is modeled by the function

h(t)=-16t^2+48t+2 (see attachment)

Answer 1

A)

At t = 3/2

B)

36 feet

Explanation:

The soccer ball is modeled by the function:

`h(t)=-16t^2+48t`

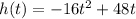
Where h(t) represents the height in feet of the ball over time t.

Note that this is a quadratic equation.

Part A)

Since this is a quadratic, the maximum height will be reached when the ball reaches its vertex.

So, we will find the x-coordinate of the vertex.

The vertex is given by:

`\displaystyle \Big (-(b)/(2a) , h( -(b)/(2a) ) \Big)`

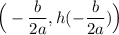
In this case, a = -16 and b = 48. Thus, the t-coordinate is:

`\displaystyle t=-(48)/(2(-16))=-(48)/(-32)=(3)/(2)`

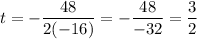
The ball will reach is maximum height at t = 3/2.

Part B)

To find the maximum height, we can simply substitute the value back into the function and evaluated. Therefore:

`\displaystyle\begin{aligned} h((3)/(2))&=-16\Big((3)/(2)\Big)^2+48\Big((3)/(2)\Big)\\\\ &=-16\Big((9)/(4)\Big)+24(3)\\ \\ &=-36+72\\\\ &= 36 \end{aligned}`

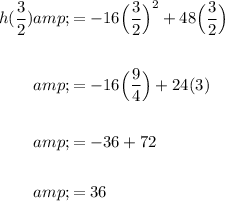
The maximum height of the ball is 36 feet.