Question

An electric field, E=-3.50x 10⁻⁸i and 5.00 x 10⁻⁸j N/C, exists at the origin of a cartesian plane.

What acceleration (magnitude and direction) does an alpha particle (information provided on the formula sheet) experience if placed at the origin? Give your answer in polar form.

Answer 1

The force (F) experienced by a charged particle in an electric field is given by Coulomb's law: F = q · E. The magnitude and direction of the acceleration in polar form are approximately 1.93 × 10⁻⁷ m/s² at an angle of -53.13°.

Step-by-step explanation:

The force (F) experienced by a charged particle in an electric field is given by Coulomb's law:

F = q · E

where:

- F is the force,

- q is the charge of the particle,

- E is the electric field.

The acceleration (a) of the particle is related to the force by Newton's second law:

F = m · a

where:

- m is the mass of the particle,

- a is the acceleration.

Combining these equations, we get:

a =
`(q \cdot E)/(m)`

Given that an alpha particle has a charge (q) of +2e (where e is the elementary charge) and a mass (m) of 6.64 × 10⁻²⁷ kg, and the electric field (E) is provided as -3.50 ×10⁻⁸i + 5.00 × 10⁻⁸j\) N/C, we can substitute these values into the equation.

a =
`((2e) \cdot (-3.50 * 10^(-8)i + 5.00 * 10^(-8)j))/(6.64 * 10^(-27))`

Now, we need to calculate the magnitude and direction of the acceleration in polar form.

The magnitude of the acceleration ( |a| ) is given by:

|a| =
`√((a_x)^2 + (a_y)^2)`

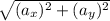
where
`\(a_x\)` and
`\(a_y\)` are the components of acceleration in the x and y directions.

|a| =
`\sqrt{(-3.50 * 10^(-8))^2 + (5.00 * 10^(-8))^2}`

|a| =
`\sqrt{1.225 * 10^(-15) + 2.5 * 10^(-15)}`

|a| =
`\sqrt{3.725 * 10^(-15)}`

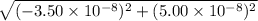
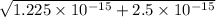
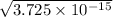
|a| ≈ 1.93 × 10⁻⁷ m/s²

The direction of the acceleration (θ) is given by:

θ = tan⁻¹
`\left((a_y)/(a_x)\right)`

θ = tan⁻¹
`\left((5.00 * 10^(-8))/(-3.50 * 10^(-8))\right)`

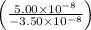
θ ≈ -53.13°

Therefore, the magnitude and direction of the acceleration in polar form are approximately 1.93 × 10⁻⁷ m/s² at an angle of -53.13°.