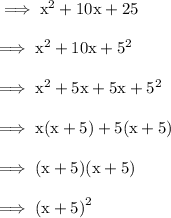Answer:
- The perfect square trinomial is x² + 10x +

- The factored perfect square trinomial is
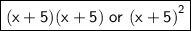
Explanation:
Given:
Binomial: x² + 10x
To Find:
- Constant that should be added to the binomial so that it becomes a perfect square trinomial.
- Factor the trinomial.
Solution:
To find the constant we would compare the binomial with (a + b)² i.e. a² + 2ab + b² as it is the formula for perfect square.
By comparing we get:
a² = x²
2ab = 10x
b² = constant (To find out)
From this we can make out:
a = x

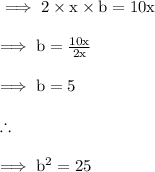
So, constant that should be added to the binomial so that it becomes a perfect square trinomial is
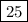 .
.
Perfect square trinomial is x² + 10x + 25
Factorisation of the trinomial: