Final Answer:
Bumper car A is going to have more energy and will bump bumper car B backward.
Step-by-step explanation:
When two objects collide, the energy involved in the collision can be calculated using the formula for kinetic energy:
![\[ KE = (1)/(2) * m * v^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zp5bh11e5rki5o1wonw2vssjxdrnc0lvkq.png)
where
 is kinetic energy,
is kinetic energy,
 is mass, and
is mass, and
 is velocity. In this scenario, both bumper cars have the same velocity
is velocity. In this scenario, both bumper cars have the same velocity
 but bumper car A has a greater mass
but bumper car A has a greater mass
 compared to bumper car
compared to bumper car
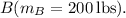
The kinetic energy of each bumper car can be calculated using the formula. Let's denote the kinetic energy of bumper car A as
 and bumper car B as
and bumper car B as
 :
:
![\[ KE_A = (1)/(2) * m_A * v^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/z7c7dwasqfpqt8s50mqwoznw287fezvmb0.png)
![\[ KE_B = (1)/(2) * m_B * v^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nk7docubb55wx0mlfpbqfy3wzwm113n7ti.png)
Since
 , bumper car A will have a higher kinetic energy. The kinetic energy represents the capacity to do work, and in a collision, the car with higher kinetic energy tends to impart more force on the other car. Therefore, bumper car A, with its greater mass, will have more energy and bump bumper car B backward in the collision.
, bumper car A will have a higher kinetic energy. The kinetic energy represents the capacity to do work, and in a collision, the car with higher kinetic energy tends to impart more force on the other car. Therefore, bumper car A, with its greater mass, will have more energy and bump bumper car B backward in the collision.
In summary, the collision outcome is influenced by the kinetic energy, which is determined by both mass and velocity. Bumper car A, being heavier, will have more energy and push bumper car B backward in the collision.