Final Answer:
Each side of the equilateral triangle is
 , so each side is
, so each side is
 cm.
cm.
Step-by-step explanation:
In an equilateral triangle, all sides are equal, and each angle measures 60 degrees. The altitude of the triangle bisects one of the angles, forming a right-angled triangle with half the equilateral side as the base, the altitude as one leg, and the side of the equilateral triangle as the hypotenuse.
Using the Pythagorean theorem, we find that the length of one side s is given by:
![\[ s = \sqrt{\text{altitude}^2 + \left((s)/(2)\right)^2} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8jeas8szihtk24o1awu2v365th2vm87ura.png)
Substituting the given altitude value
 , we get:
, we get:
![\[ s = \sqrt{12^2 + \left((s)/(2)\right)^2} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lz7qjorv6fd7jv8bufj9ujqkqpje5fevw3.png)
Solving this equation yields
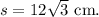
Understanding the relationship between the altitude, sides, and angles of an equilateral triangle is fundamental in geometry, providing a basis for solving various geometric problems.