The equation
 represents a parabola that opens to the left with a vertex at (-4, 0) when rearranged in standard form.
represents a parabola that opens to the left with a vertex at (-4, 0) when rearranged in standard form.
The equation given is
 . To understand which graph is represented by this equation, we can rearrange it to complete the square for y. Here are the steps:
. To understand which graph is represented by this equation, we can rearrange it to complete the square for y. Here are the steps:
First, factor out the 5 from the y terms:
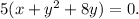
Now, complete the square on the y terms:
 is a perfect square trinomial
is a perfect square trinomial
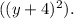
Subtract 16 from both sides to keep the equation balanced:

Rewrite the equation:
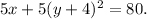
Divide by
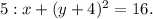
Finally, rearrange to reveal the form of a shifted circle:

This is the equation of a parabola that opens to the left with vertex at (-4, 0) and a horizontal axis of symmetry. So, the correct graph would be that of a leftward-opening parabola.