Answer:
h =
 b =
b =
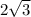
Explanation:
In mathematics, there are these special triangle rules called, the "45-45-90" triangle and the "30-60-90" triangle. These special triangles have unique rules that define their hypotenuse, side-lengths, angles, and more.
For the first one, it is a 45-45-90 triangle. The legs of this triangle are of the same length. Let x be the value of the leg. Using the Pythagorean theorem, we can identify the side length by this: 1^2 + 1^2 = sqrt-2. That is if x is 1. But what if it isn't? Well, it is simply (sqrt-2) * x. Pythagorean theorem is a great way to double-check the answer, but know these rules are important in Geometry and beyond. In this case, we're given the value of one of the legs as 5 units. Using the identity, we can say that h is equal to (sqrt-2) * 5. Ultimately, it simplifies to h is equal to 7.07 approximately. You can leave it as sqrt-2 times 5 if you want the exact value.
For the second one, it is a 30-60-90 triangle. The legs of this triangle have this ratio: the shorter one is x, the longer one is sqrt-3 * x. With this, we can apply the Pythagorean theorem again to find the hypotenuse, assuming x is 1. If x is 1 and sqrt-x is sqrt-3, then that means the hypotenuse is sqrt-4, which is 2. If that is the case, then the short leg is 3 / sqrt-3. which is sqrt-3. Now that we know the length of the short leg, it is easier to find the length of the hypotenuse. Multiply the short leg by 2. That gives us 2 times the root 3.