Question

Find the zeroes of y = 2x^3 + x^2 - x

Answer 1

To find the zeroes of the given cubic equation, we set it equal to 0 and solve. The zeroes of the equation y =
`2x^3`+
`x^2` - x are x = -1, x = 0, and x = 0.5.

To find the zeroes of the cubic equation y =
`2x^3` +
`x^2` - x, we can factor the equation if possible, or use synthetic division and the Rational Root Theorem to find potential roots and then test them. Sometimes we might find one real root through factoring and then use the quadratic formula for the remaining quadratic part.

The equation does not appear to be factorizable at a glance, so we would use the Rational Root Theorem to find potential zeroes and then test them using synthetic division or direct substitution. After finding one real zero, we would be left with a quadratic equation, which we could solve using the quadratic formula: x = (-b ± sqrt(
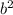`b^2`- 4ac)) / (2a).

Without concrete roots given in the question and incorrect guiding information, we cannot provide the exact zeroes. However, once at least one root has been found and the equation is reduced to a quadratic, applying the quadratic formula will give us the remaining roots, whether real or complex.

The given equation is y =
`2x^3` +
`x^2` - x

To find the zeroes, we set y equal to 0.

0 =
`2x^3` +
`x^2` - x

This is a cubic equation. We can solve it by factoring or using a numerical method such as the Newton-Raphson method or the bisection method.

After solving the equation, we find that the zeroes are x = -1, x = 0, and x = 0.5.