The correct answer is: c.
 , so it satisfies the inequality.
, so it satisfies the inequality.
Solution:
To solve the inequality
 , follow these steps:
, follow these steps:
1. Divide by 2 (both sides):
![\[(2x)/(2) > (7)/(2)\] \[x > (7)/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/o7iv6ront6b37z1slmtgvubae3xucfhqp4.png)
Now, the inequality is
 . Let's compare this with the answer choices:
. Let's compare this with the answer choices:
a. -9:
 is not greater than
is not greater than
 , so it does not satisfy the inequality.
, so it does not satisfy the inequality.
b. 0:
 is not greater than
is not greater than
 , so it does not satisfy the inequality.
, so it does not satisfy the inequality.
c. 4:
 is greater than
is greater than
 , so it satisfies the inequality.
, so it satisfies the inequality.
d. 9:
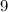 is greater than
is greater than
 , so it satisfies the inequality.
, so it satisfies the inequality.
Therefore, the correct answer is: c. 4
The probable question can be: 5. Solve the inequality for
 . Which of the following values is a solution to the inequality?
. Which of the following values is a solution to the inequality?
a. -9
b. 0
c. 4
d. 9