Question

A carpenter purchased 50 ft of redwood and 70 ft of pine for a total cost of $258. A second purchase, at the same prices, included 90 ft of redwood and 60 ft of pine for a total cost of $372. Find the cost per foot of redwood and of pine.

Answer 1

• redwood: $3.20 per foot
• pine: $1.40 per foot

Explanation:

The two purchases can be described by the equations ...

50r +70p = 258

90r +60p = 372

Rewriting these equations in general form facilitates the use of the cross-multiplication method of solving them.

50r +70p -258 = 0

90r +60p -372 = 0

According to the cross-multiplication method, we need three cross-products:

∆1 = (50)(60) -(90)(70) = -3300

∆2 = (70)(-372) -(60)(-258) = -10560

∆3 = (-258)(90) -(-372)(50) = -4620

The solutions are the solutions to the equations ...

1/∆1 = t/∆2 = p/∆3

r = ∆2/∆1 = -10560/-3300 = 3.20

p = ∆3/∆1 = -4620/-3300 = 1.40

The cost per foot of the redwood was $3.20; of the pine, $1.40.

_____

Additional comment

Here's how this version of the "cross-multiplication" method works. For equations ...

• ax +by +c = 0
• dx +ey +g = 0

a coefficient array can be written as ...

`\left[\begin{array}{cccc}a&b&c&a\\d&e&g&d\end{array}\right]`

The cross-products of interest are formed from adjacent columns:

`\Delta1=ac-db\\\Delta2=bg-ec\\\Delta3=cd-ga`

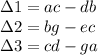
and the solutions are ...

`x=(\Delta2)/(\Delta1),\quad y=(\Delta3)/(\Delta1)`

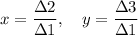
Using this method requires no more arithmetic operations than solving by substitution or elimination, and may require fewer: 6 products, 3 sums, and 2 quotients are needed.