Question

a gold mine is projected to produce $30,000 during its first year of operation, $27,000 the second year, $24,000 the third year, and so on. if the mine is expected to produce for a total of 8 years, and the effective annual interest rate is 4%, its present worth is nearest to

Answer 1

the effective annual interest rate is 4%, its present, worth is nearest to $28,846. Option d is the right choice.

To find the present worth of the gold mine, we need to calculate the present value of the cash flow generated by the mine.

Since the cash flow is decreasing each year, we can use the formula for the sum of a geometric series.

The formula is
PV =
`(CF)/((1 + r))+ (CF)/((1 + r)^2) +----+(CF)/((1 + r)^n)`
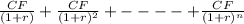
where PV is the present value, CF is the cash flow, r is the interest rate, and n is the number of years.

In this case, the cash flow in the first year is $30,000, and it is decreasing by $3,000 each year.

The interest rate is 4%. So the present value is calculated as follows:

1. PV =
   `\frac{30,000} { (1 + 0.04) }+ \frac{ 27,000} { (1 + 0.04)^2} + \frac{24,000 } {(1 + 0.04)^3} + ... + \frac{15,000} {(1 + 0.04)^8}`
2. PV =
   `\frac {30,000} { 1.04} + \frac {27,000} { 1.04^2 }+ \frac {24,000} { 1.04^3} + ... + \frac {15,000} { 1.04^8}`
3. PV =
   `(30,000 )/(1.04) + (27,000)/( (1.04 *1.04) )+ \frac{24,000} {(1.04 *1.04 * 1.04) }+ ... + \frac{15,000} { (1.04 *1.04 * 1.04*1.04*1.04*1.04 *1.04*1.04)}`
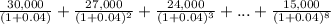
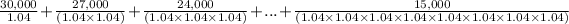
4. PV ≈ $28,846.15

Therefore, the present worth of the gold mine is approximately $28,846.1

Option d is the right choice.

question:

A gold mine is projected to produce $30,000 during its first year of operation, $27,000 the second year $24,000 the third year, and so on. If the mine is expected to produce for a total of 8 years, and the effective annual interest rate is 4%, its present, worth is nearest to _____

a) $130,342

b) $132.747

c) $135,439

d) $28,846