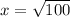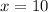Answer:
10 blocks
Explanation:
Given
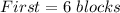
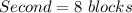 east
east
Required
Determine the shortest possible distance
To better explain my solution, I've added an attachment that illustrates her movement.
Using the attachment as a point of reference, the shortest distance is calculated by calculating the length of the hypotenuse using Pythagoras theorem.
So, we have:
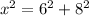
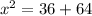
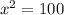
Take positive square root of both sides