Question

a project requires an initial investment of $1 million right now, and returns 11 payments of $0.3 million over the next 11 years. the first payment is next year. what is the npv of this project if the appropriate cost of capital is 7%?

Answer 1

The Net Present Value (NPV) of the project, considering an initial investment of $1 million and 11 payments of $0.3 million over 11 years with a 7% cost of capital, is $1,992,200.

The formula for NPV is:

`\[ NPV = \sum_(t=0)^(n) \frac{{CF_t}}{{(1 + r)^t}} - Initial Investment \]`

Where:

`\( CF_t \) = Cash flow at time \( t \)`

`\( r \) = Discount rate (cost of capital)`

`\( n \) = Number of periods`

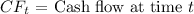
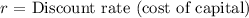
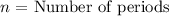
Given:

Initial investment = $1 million

Cash flow per period = $0.3 million for 11 years

Discount rate (cost of capital) = 7%

calculate the NPV:

`\[ NPV = -1,000,000 + \sum_(t=1)^(11) \frac{300,000}{{(1 + 0.07)^t}} \]`

`\[ NPV = -1,000,000 + 300,000 * \left( (1 - (1 + 0.07)^(-11))/(0.07) \right) \]`

Calculating this:

`\[ NPV = -1,000,000 + 300,000 * \left( (1 - 0.5084)/(0.07) \right) \]`

`\[ NPV = -1,000,000 + 300,000 * 9.974 \]`

`\[ NPV = -1,000,000 + 2,992,200 \]`

`\[ NPV = 1,992,200 \]`

Therefore, the Net Present Value (NPV) of this project, given a 7% cost of capital, is $1,992,200.