At a 0.05 significance level, we don't have adequate proof to dismiss the claim that 16% of US adults prefer curling as their top winter Olympic sport. Yet, this conclusion relies on a sample and might not represent the actual population proportion.
How to solve
Null Hypothesis (H ₀): The proportion of US adults who say curling is their favorite winter Olympic sport is 16%.
Alternative Hypothesis (H₁): The proportion of US adults who say curling is their favorite winter Olympic sport is different from 16%.
Level of Significance (α): 0.05
Sample Size (n): 300
Sample Proportion (p): 20%
Test Statistic:
We will use the z-statistic to test this hypothesis. The formula for the z-statistic is:
z =
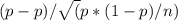
where:
p is the sample proportion (20%)
p is the population proportion (16%)
n is the sample size (300)
Calculating the z-statistic:
z =

z ≈ 1.73
Decision Rule:
We will reject the null hypothesis if the z-statistic falls outside the critical region. At a level of significance of 0.05 and a two-tailed test, the critical region consists of values less than -1.96 or greater than 1.96.
Decision:
Our calculated z-statistic (1.73) is within the critical region (between -1.96 and 1.96). Therefore, we fail to reject the null hypothesis.
At a 0.05 significance level, we don't have adequate proof to dismiss the claim that 16% of US adults prefer curling as their top winter Olympic sport. Yet, this conclusion relies on a sample and might not represent the actual population proportion.