Question

a cup of jello is inserted into a cup holder attached to one end of a horizontal aluminum beam. the beam is 2.1 m long. the other end of the beam is attached to a pivot. a motor rotates the beam about the pivot, in the horizontal plane, at constant speed. at what rotation rate (in revolutions per second) will the centripetal acceleration of the jello be approximately 3.1g (where g is the acceleration of earth's gravity)?

Answer 1

To find the rotation rate at which the centripetal acceleration of the jello will be approximately 3.1g, we can use the formula for centripetal acceleration. The rotation rate is approximately 0.606 revolutions per second.

Step-by-step explanation:

To find the rotation rate at which the centripetal acceleration of the jello will be approximately 3.1g, we need to use the formula for centripetal acceleration:

`a = (v^2) / r`
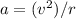
where a is the centripetal acceleration, v is the linear velocity, and r is the radius of the circular path.
In this case, we know that a = 3.1g, where g is the acceleration due to gravity. We can convert g to
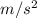`m/s^2` by multiplying it by
`9.8 m/s^2.` The radius of the circular path is 2.1 m.
Using these values, we can rearrange the formula to solve for v:
v = sqrt(a * r)
Substituting the known values:
v = sqrt((3.1 * 9.8) * 2.1)
v ≈ 7.988 m/s
Since we are looking for the rotation rate in revolutions per second, we can divide v by the circumference of the circular path:
rotation rate = v / (2 * pi * r)
rotation rate ≈ 7.988 / (2 * 3.14 * 2.1)
rotation rate ≈ 0.606 revolutions per second
Therefore, the rotation rate at which the centripetal acceleration of the jello will be approximately 3.1g is approximately 0.606 revolutions per second.