Question

a ball travels on a parabolic path in which the height (in feet) is given by the expression , where is the time after launch. at what time is the height of the ball at its maximum?

Answer 1

The ball reaches its greatest height 1.5 units of time after launch.

Assume we have a quadratic function with the structure as follows:

h(t) =
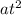`at^(2)`+ bt + c

The maximum value of h(t) will occur at the point if t is negative.

`t_(MAX)` = -
`(b)/(2a)`

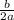
In this query:

h(t) =
`-25t^(2)` +75t +24

Thus

a= -25

b= 75

c= 24

Next

`t_(MAX)`=
`(b)/(2a)` = -
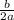`(75)/(2*(-25))` = 1.5

Question

A ball travels on a parabolic path in which the height (in feet) is given by the expression $-25t^2+75t+24$, where $t$ is the time after launch. At what time is the height of the ball at its maximum?