Question

a piece of charcoal is found tocontain 30% of the carbon-14 that it originally had. when didthe tree die from which the charcoal came? use 5730 yearsas the half-life of carbon-14.

Answer 1

The result is approximately 5,023 years. Therefore, the tree from which the charcoal came died about 5,023 years ago.

Radiocarbon dating can estimate the age of organic materials by analyzing the decay of carbon-14 isotopes.

Carbon-14 undergoes radioactive decay with a half-life of approximately 5,730 years.

In the case of the charcoal sample, it is found to contain only 30% of the original carbon-14.

This reduction in carbon-14 concentration indicates elapsed time since the death of the organism from which the charcoal originated.

The formula for radioactive decay is given by the equation:

`N_(t)` =
`N_(0)` ×
`(1)/(2)^{(t)/(T) }`

Where:

`N_(t)` is the final amount of carbon-14,

`N_(0)` is the initial amount of carbon-14,

t is the elapsed time,

T is the half-life of carbon-14.​

Given that
`N_(t)`= 0.3
`N_(0)` (30% of the original amount), we can substitute these values into the equation:

0.3
`N_(0)` =
`N_(0)` ×
`(1)/(2)^{(t)/(5730) }`

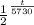
Solving for t (time), we find:

`{(t)/(5730) }` =log 2 (0.3)

t= 5730 × log2 (0.3)

Using this formula, we can calculate the elapsed time since the death of the tree. The result is approximately 5,023 years.

Therefore, the tree from which the charcoal came died about 5,023 years ago.

Question

Estimating the Age of a Tree A piece of charcoal is found to contain 30% of the carbon - 14 that it originally had. When did the tree die from which the charcoal came? Use 5730 years as the half-life of carbon - 14.