Question

Graph a right triangle with the two points forming the hypotenuse. Using the sides, find the

distance between the two points in simplest radical form.
(-2,-4) and (3,8)
-10

Answer 1

The distance between the two points (- 2, - 4) and (3, 8) is equal to 13 units.

How to find the length of a hypotenuse

In this problem we must determine the length of the hypotenuse of a right triangle, this can be done by applying Pythagorean theorem:

`d = √((\Delta x)^2 + (\Delta y)^2)`

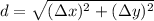
Where:

• d - Distance
• Δx - Change along x-axis.
• Δy - Change along y-axis.

If we know that P₁(x, y) = (- 2, - 4) and P₂(x, y) = (3, 8), then the distance of the hypotenuse is:

`d = √([3 - (- 2)]^2+[8 - (- 4)]^2)`

`d = √(5^2+12^2)`

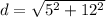
d = √169

d = 13

By Pythagorean theorem, the hypotenuse of the right triangle has a length of 13 units.