The length of the guy wire required for the communications tower is approximately 247 meters when rounded to the nearest meter.
To find the length of the cable required for the guy wire, we can use trigonometric methods. We are given:
1. The angle of inclination of the hill:
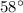
2. The angle of the guy wire with respect to the ground:
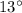
3. The distance from the base of the tower to the point where the guy wire is attached to the ground:
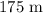
The angle between the guy wire and the hill will be the difference between the angle of inclination and the angle of the guy wire with respect to the ground. This is because the angle of inclination and the angle of the guy wire with respect to the ground form a supplementary pair with the angle between the hill and the guy wire.
Step 1: Find the angle between the guy wire and the hill.
![\[ \text{Angle} = 58^\circ - 13^\circ = 45^\circ \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/jylhaaw4urcymd2jdy0b.png)
Step 2: Use the trigonometric function to find the length of the guy wire.
We'll use the cosine function since we have the adjacent side (the distance along the hill) and we want to find the hypotenuse (the length of the guy wire).
![\[ \cos(\text{Angle}) = \frac{\text{Adjacent}}{\text{Hypotenuse}} \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/gzvg8vcq2na2tikgpcjr.png)
![\[ \cos(45^\circ) = \frac{175 \text{ m}}{\text{Hypotenuse}} \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/fzcrz0j5rty4q71skzvl.png)
Step 3: Solve for the hypotenuse (the length of the guy wire).
![\[ \text{Hypotenuse} = \frac{175 \text{ m}}{\cos(45^\circ)} \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/drrykzlt3j22zb2y7vwq.png)
Step 4: Calculate the length of the guy wire.
Since
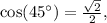 the equation becomes:
the equation becomes:
![\[ \text{Hypotenuse} = \frac{175 \text{ m}}{(√(2))/(2)} \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/haql8cfkrz077xmzovwd.png)
![\[ \text{Hypotenuse} = 175 \text{ m} * (2)/(√(2)) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/77ikn5tfj4a28oipp1tz.png)
= 247 meter( rounded to the nearest meter)