Question

The common ratio in a geometric sequence is 3/2, and the fifth term is 1. Find an

Answer 1

First term: a1 = 16/81

Equation of the geometric sequence:
`a_(n)=(16/81)(3/2)^(^n^-^1^)`

Explanation:

Are you looking for equation of the geometric sequence or the first term.

My work below will help you find both:

1. the first term,
2. and the equation of the geometric sequence (given the common ratio, the fifth term, and the first term we'll find).

----------------------------------------------------------------------------------------------------------Formula for the nth term of a geometric sequence:

The formula for the nth term of a geometric sequence is given by:

`a_(n)=a1*r^(^n^-^1^)`, where:

• an is the nth term,
• a1 is the first term
• r is the common ratio,
• and n is the term position (e.g., first, fifth, etc.).

Finding a1:

We can find a1 by substituting 1 for an, 3/2 for r, and 5 for n in the formula for the nth term of a geometric sequence:

`1=a1(3/2)^(^5^-^1^) \\\\1=a1(3/2)^4\\\\(1=a1*(81/16)) / (81/16)\\\\(1=a1*(81/16))*(16/81)\\\\16/81=a1`

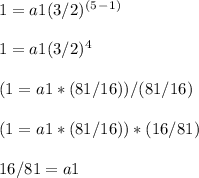
Therefore, the first term is 16/81.

Writing the equation of the geometric sequence:

Since we know that:

• the first term is 16/81,
• and that the common ratio is 3/2,

the equation to find the nth term of the geometric sequence is given by:

`a_(n)=(16/81)(3/2)^(^n^-^1^)`