Question

Need help with this question

Answer 1

The equation of the parabola in vertex form x - 5 = - (y + 1)².

How to derive the equation of a parabola

Herein we find the graphic representation of a parabola, whose axis of symmetry is parallel with x-axis. Vertex form of the equation of the parabola is introduced below:

x - h = C · (y - k)²

Where:

• h, k - Coordinates of the vertex.
• C - Vertex constant.

Now we proceed to determine the equation of the parabola:

First, find the vertex of the parabola:

Vertex: (h, k) = (5, - 1)

Second, compute the vertex constant of the parabola:

Vertex constant:

`C = (x-h)/((y - k)^2)`

`C = (4-5)/((0+1)^2)`

`C = -(1)/(1)`

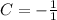
C = - 1

Third, write the vertex form of the parabola:

x - 5 = - (y + 1)²