Question

The perimeter of the quadrilateral is 40 centimeters. Find the length of each side. Side one=x 3=

Answer 1

The lengths of the sides of the quadrilateral are

Side one: x+8=4+8=12 centimeters

Side two: x+7=4+7=11 centimeters

Side three: x² −2x = −2(−7)=53 centimeters

Side four: 3x−3=3(4)−3=9 centimeter

We are given that the perimeter of the quadrilateral is 40 centimeters. This means that the sum of the lengths of the four sides is 40 centimeters. We can represent the lengths of the sides of the quadrilateral using variables. Let:

Side one be represented by x+8

Side two be represented by x+7

Side three be represented by x² - 2x

Side four be represented by 3x−3

We can now set up an equation to represent the given information:

x+8+x+7+x²−2x+3x−3=40

Simplifying the equation, we get:

x²+3x+12=40

Subtracting 40 from both sides, we get:

x²+3x−28=0

Using the quadratic formula, we can solve for x:

`x = \frac{-b \sqrt{b^(2 - 4ac) } }{2a}`

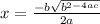
Plugging in the values of a, b, and c, we get:

`x = \frac{-3 \sqrt{3^(2 - 4 -28) } }{2}`

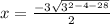
x = -3±√121/2

Solving for x, we get:

x=4 or x=−7

Therefore, the lengths of the sides of the quadrilateral are

Side one: x+8=4+8=12 centimeters

Side two: x+7=4+7=11 centimeters

Side three: x² −2x = −2(−7)=53 centimeters

Side four: 3x−3=3(4)−3=9 centimeters

Complete question:

The perimeter of the quadrilateral is 40 centimeters. Find the length of each side.

Side one = x + 8 =

Side two = x + 7 =

Side three = x² – 2x =

Side four = 3x - 3 =