Question

In a right triangle, the measures of the legs are x and x + 14 and the measure of the hypotenuse is x + 16. Find the measure of x.

Answer 1

`x=10`

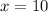
Explanation:

We can use the Pythagorean Theorem:

`a^2+b^2=c^2`

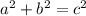
The two legs are x and (x + 14) and the hypotenuse is (x + 16). Therefore:

`(x)^2+(x+14)^2=(x+16)^2`

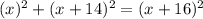
Expand:

`\displaystyle x^2+(x^2+28x+196)=x^2+32x+256`

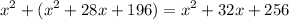
Combine like terms:

`2x^2+28x+196=x^2+32x+256`

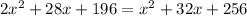
Subtract the right from the left:

`(2x^2+28x+196)-(x^2+32x+256)=0`

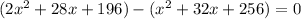
Subtract:

`x^2-4x-60=0`

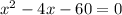
Factor:

`(x-10)(x+4)=0`

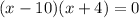
Zero Product Property:

`x-10=0\text{ or } x+4=0`

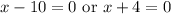
Solve:

`\displaystyle x = 10 \text{ or } x = -4`

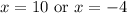
The x cannot be negative since a side cannot measure -4. So, our only answer is:

`x=10`

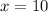
So, the legs are 10 and 24 with the hypotenuse being 26.