Question

A mass on a string of unknown length oscillates as a pendulum with a period of 6.0 s. What is the period if the string length is doubled?

Answer 1

The period of the pendulum, when the string length is doubled, is approximately 8.5 s.

The period of a simple pendulum, the time it takes to complete one full oscillation, is determined by the formula
`T=2\pi √(L/g)`, where T is the period, L is the length of the string, and g is the acceleration due to gravity.

In the given scenario, the original period of the pendulum is T1​=6.0 seconds. If the string length is doubled, the new length becomes 2L. Substituting this into the pendulum period formula, we get
`T_2=2\pi √(2L/g)`

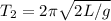
Comparing the two periods, we find that
`T_2/T_1=√(2)` . Therefore, the new period T_2 when the string length is doubled is approximately 6.0s×
`√(2)`, yielding T_2≈8.5 seconds. The longer string results in a longer period, reflecting the dependency of the pendulum's period on the square root of the string length.