Question

Determine the values of a and b

Answer 1

a = 16°

b = 148°

Explanation:

From observation of the given diagram:

• Line segment AB is the radius of circle A.
• The line intersecting the circle at point B is a tangent line to circle A.

As the tangent line to a circle is always perpendicular to the radius at the point of tangency, the measure of angle ABD is 90°.

The measure of angle a is the difference between ∠CBD and ∠ABD. Given that m∠CBD = 106°, then:

`a=m\angle BCD - m\angle ABD`

`a=106^(\circ) - 90^(\circ)`

`a=16^(\circ)`

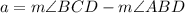
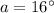
Triangle ABC is an isosceles triangle, since two of its side lengths (AB and AC) are the radii of the circle. As m∠a = 16°, this means that m∠ACB = 16°. Interior angles in a triangle sum to 180°, so to find the measure of angle b, simply subtract the measures of ∠a and ∠ACB from 180°:

`b=180^(\circ)-m\angle a-m\angle ACB`

`b=180^(\circ)-16^(\circ)-16^(\circ)`

`b=148^(\circ)`

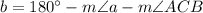
In conclusion, the values of a and b are:

• a = 16°
• b = 148°

Answer 2

The calculated values of a and b are a = 16 and b = 148

How to determine the values of a and b

From the question, we have the following parameters that can be used in our computation:

The circle

The angle between the radius of a circle and the tangent line is 90 degrees

So, we have the following equation

a + 90 = 106

Evaluate

a = 16

The sum of angles in a triangle is 180 degrees

So, we have

b = 180 -2 * 16

Evaluate

b = 148

Hence, the values of a and b are a = 16 and b = 148