Question

The baseball concession stand sold 12 hotdogs sold in three games. Which proportion could be used to make the best estimate for the number of games it would take to sell 864 hotdogs?

Answer 1

To determine the number of games it would take to sell 864 hotdogs, given that 12 hotdogs are sold in three games, we set up a proportion and find that it would take 216 games to sell 864 hotdogs at the same rate.

Step-by-step explanation:

The question is asking for a proportion to estimate the number of games needed to sell a certain amount of hotdogs. Given that 12 hotdogs are sold in three games, we can set up the proportion as follows:

`\(\frac{12\text{ hotdogs}}{3\text{ games}} = \frac{864\text{ hotdogs}}{x\text{ games}}\)`

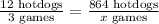
To solve for \(x\), we cross-multiply:

12 * x = 3 * 864

`x = \((3 * 864)/(12)\) x = \((2592)/(12)\)`

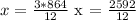
x = 216

Therefore, it will take 216 games to sell 864 hotdogs at the same rate.