Question

Pt of where im stuckk!!!!!

Answer 1

The equation of the parabolas, obtained using the standard form and vertex forms of the equation of a parabola are;

`\begin{tabular} \cline{1-2}Parabola &Equation \\ \cline{1-2}\#1 &y = -0.25\cdot x^2 - x + 3\\\cline{1-2}\#2 &y = (1/3)\cdot (x + 6)^2 + 1 \\\cline{1-2}\#3 &y = (-1/6)\cdot (x - 3)^2+6 \\\cline{1-2}\end{tabular}`

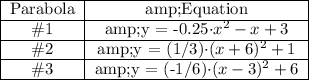
The equations of the parabola are found as follows;

Challenge #8

The coordinates of the points on the graph are;

(-6, 0), (-4, 3), and (2, 0)

The form of the quadratic equation is; f(x) = a·x² + b·x + c

Plugging in the above x and y-values, where the ordered pairs are presented in (x, y) value format, we get;

Where (x, y) = (-6, 0)

f(-6) = a × (-6)² + b × (-6) + c

f(-6) = 0, therefore;

a × (-6)² + b × (-6) + c = 0

36·a - 6·b + c = 0...(1)

Where (x, y) = (-4, 3)

f(-4) = a × (-4)² + b × (-4) + c

f(-4) = 3, therefore;

a × (-4)² + b × (-4) + c = 3

16·a - 4·b + c = 3...(2)

Where (x, y) = (2, 0)

f(2) = a × 2² + b × 2 + c

f(2) = 0, therefore;

a × 2² + b × 2 + c = 0

4·a + 2·b + c = 0...(3)

Therefore;

36·a - 6·b + c = 0

16·a - 4·b + c = 3

4·a + 2·b + c = 0

The system of three equations can be evaluated using an online tool to get;

a = -1/4, b = -1, and c = 3

Therefore, the quadratic equation is; y = -0.25·x² - x + 3

The above points can be plotted on a spreadsheet

The Polynomial Trendline of degree 2, obtained adding the Chart Element using MS Excel indicates that the equation of the parabola that passes through the point is; y = -0.25·x² - x + 3

Challenge #9; The shape of the points indicates that the vertex of the parabola is the point; (-6, 1)

The vertex form of the equation of a parabola is; y = a·(x - h)² + k

Therefore, we get; (h, k) = (-6, 1)

y = a·(x - (-6))² + 1

y = a·(x + 6)² + 1

The point (-3, 4) indicates that we get;

4 = a·((-3) + 6)² + 1

4 = 9·a + 1

a = (4 - 1)/9

a = 1/3

The equation of the parabola is therefore;

y = (1/3)·(x + 6)² + 1

Challenge #10

The points on the parabola are;

(-3, 0), (0, 4.5), (3, 6), and (9, 0)

The horizontal distance from the point (3, 6) to the points on the x-axis, (-3, 0), and (9, 0), are the same, therefore, the line of symmetry passes through the point (3, 6), which is therefore, the vertex of the parabola, and we get;

y = a·(x - 3)² + 6

The point (0, 4.5) indicates that we get;

4.5 = a·(0 - 3)² + 6

4.5 = 9·a + 6

9·a = 4.5 - 6

a = -1.5/9

-1.5/9 = -1/6

The equation of the parabola is therefore; y = (-1/6)·(x - 3)² + 6