The P-value is approximately 0.105.
Null hypothesis will not be rejected
In general, based on the result of the analysis, first sons are approximately the same height as their fathers.
How to test the claim that there is no difference in heights between fathers and their first son
To test the claim that there is no difference in heights between fathers and their first son, perform a paired t-test.
The null hypothesis, denoted as H₀, states that there is no difference in heights, while the alternative hypothesis, denoted as H₁, suggests that there is a difference.
To calculate the test statistic and P-value for the paired t-test, use the provided height data:
Height of father: 72, 66, 69, 70, 70, 70, 70, 75, 65, 65
Height of son: 74, 68, 69, 71, 72, 70, 72, 74, 65, 65
Calculate the differences between the heights of fathers and sons:
Height difference = Height of son - Height of father
74-72, 68-66, 69-69, 71-70, 72-70, 70-70, 72-70, 74-75, 65-65, 65-65
2, 2, 0, 1, 2, 0, 2, -1, 0, 0
Calculate the sample mean difference (
 ):
):
 = (sum of height differences) / (number of observations)
= (sum of height differences) / (number of observations)
= (2 + 2 + 0 + 1 + 2 + 0 + 2 - 1 + 0 + 0) / 10
= 8 / 10
= 0.8
Calculate the standard deviation of the differences (sᵈ):
sᵈ = sqrt((sum of squared differences) / (n - 1))
=
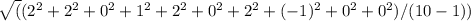
=
 ((4 + 4 + 0 + 1 + 4 + 0 + 4 + 1 + 0 + 0) / 9)
((4 + 4 + 0 + 1 + 4 + 0 + 4 + 1 + 0 + 0) / 9)
=
 (18/9)
(18/9)
=
 (2)
(2)
Calculate the test statistic:
T = (
 - μ₀) / (sᵈ / √n)
- μ₀) / (sᵈ / √n)
= (0.8 - 0) / (
 (2) /
(2) /
 (10))
(10))
= 0.8 / (
 (2/10))
(2/10))
≈ 0.8 / 0.447
≈ 1.79
Determine the degrees of freedom (df) for the t-distribution:
df = n - 1
= 10 - 1
= 9
Calculate the P-value associated with the test statistic:
Using a t-distribution table, the P-value for a two-tailed test with 9 degrees of freedom and a test statistic of approximately 1.79 is approximately 0.105.
Therefore, the P-value is approximately 0.105.
Determine if the null hypothesis will be rejected:
Since the P-value (0.105) is greater than the significance level of 0.05, we fail to reject the null hypothesis.
In general, are first sons the same height as their fathers?
Based on the test results, we do not have sufficient evidence to conclude that there is a significant difference in heights between fathers and their first sons. In general, it suggests that first sons are approximately the same height as their fathers.