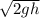Question

As part of determining the selection and installation of safety mats for a playground at a public park, the designers need to anticipate the speed of children arriving at the bottom of a long, straight plastic slide. the top end of the slide is 3.11 meters high, and the slide itself makes an angle of 39.7.

Which of the following formulas can be used to estimate the speed at which a child will arrive at the bottom of the slide?

A) \( v_f = \sqrt{2gh} \)
B) \( v_f = \sqrt{gh} \)
C) \( v_f = \sqrt{\frac{2gh}{\sin(\theta)}} \)
D) \( v_f = \sqrt{\frac{2gh}{\cos(\theta)}} \)

Answer 1

The correct formula is A) v_f =
`\sqrt{2gh`

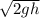
Step-by-step explanation:

To determine the speed of a child at the bottom of the slide, you can use the conservation of energy principle, where the potential energy at the top of the slide is converted into kinetic energy at the bottom.

The potential energy (PE) at the top is given by (PE = mgh), and the kinetic energy (KE) at the bottom is given by KE =1/2mv^2, where m is the mass, g is the acceleration due to gravity, (h) is the height, and (v) is the speed.

Setting the potential energy at the top equal to the kinetic energy at the bottom, you get:

mgh = 1/2mv^2

The mass (m) cancels out, and you can solve for the final velocity (v_f):

v_f =
`\sqrt{2gh`

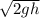
So, the correct formula is option A:

v_f =
`\sqrt{2gh`