Question

Find the domain and solve. 1/√2 x - √2 - x 1/√2 x √2 - x = 1

Options:
a. Domain: All real numbers, Solution: x = 0
b. Domain: x ≠ 0, Solution: x = 1
c. Domain: x ≠ √2, Solution: x = 1
d. Domain: All real numbers, Solution: x = 2

Answer 1

The Domain: x ≠ √2, Solution: x = 1

Step-by-step explanation:

To find the domain of the given expression, we need to identify any values of
`\( x \)` that would make the expression undefined. In this case, the expression involves a square root, and the expression under the square root cannot be negative.

The expression is
`\((1)/(√(2)x - √(2) - x) * (1)/(√(2)x √(2) - x) = 1\).`

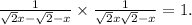
To avoid division by zero, the denominator cannot be equal to zero. Therefore,
`\( √(2)x - √(2) - x \\eq 0 \) and \( √(2)x √(2) - x \\eq 0 \).`

Solving these inequalities gives
`\( x \\eq √(2) \) and \( x \\eq 0 \).`

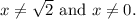
So, the domain is
`\( x \)` not equal to
`\( √(2) \)`, and the solution to the equation is found by solving the numerator, which is
`\( x = 1 \)`.

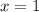Therefore, the correct option is c. Domain:
`\( x \)` not equal to
`\( √(2) \)`, Solution:
`\( x = 1 \).`