Question

Find the sum to 40 terms of the arithmetic sequence below. Please show your

work.
14+23+32

Answer 1

7580

Explanation:

The formula for the sum of an arithmatic sequence is

`(n)/(2) (a_(1) + a_(n))`,

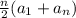where n = total number of terms (in this case 40)

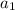`a_(1)`= the first term (in this case 14)

and
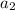`a_(2)` = the last term (we will need to find this)

to find the last term, we can use this formula:

`a_(n) = a_(1) + (n-1)d`

where d is the difference between each term (in this case 9, because 23 - 14 = 9, and 32 - 23 = 9)

thus,
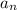`a_(n)` = 14 + (40 - 1)9 = 14 + 39*9 = 14 + 351 = 365

plug this back into the first formula to get

Σ =
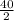`(40)/(2)` (14 + 365) = 20(379) = 7580