Question

In the pattern below, each small triangle is an

equilateral triangle with an area of 1 square unit.
a. Explain how you know that any triangle made out of
equilateral triangles will be an equilateral triangle.
b. Find the areas of the first four triangles in the pattern.
c. Describe any patterns in the areas. Predict the area
of the seventh triangle in the pattern. Explain your reasoning.

Answer 1

a. Any triangle made out of equilateral triangles will be an equilateral triangle because dividing each of its sides into equal segments and connecting midpoints produces a pattern that is an equilateral model of each component triangle.

b. The areas of the first four triangles in the pattern are 1, 4, 9, and 16 square units.

c. The patterns in the areas indicates a recursive division of the total area into smaller equilateral triangles. The area of the seventh triangle in the pattern si 49 square units.

In Mathematics and Geometry, a sequence is a series of real and natural numbers in which each term or list of elements are ordered in a particular order and repetitions are allowed.

Part a.

Generally speaking, any triangle that is made from equilateral triangles will be an equilateral triangle because dividing each of its sides into equal segments and connecting midpoints produces a pattern that is an equilateral model of each component triangle.

Part b.

Based on inductive reasoning, the patterns of the areas for the nth equilateral triangle can be modeled by the following explicit formula;

`A_n =n^2`

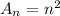
When n is 1, the area is given by;

`A_1 =1^2\\\\A_1=1\;square\;unit`

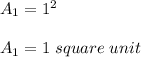
When n is 2, the area is given by;

`A_2 =2^2\\\\A_2=4\;square\;unit`

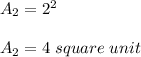
When n is 3, the area is given by;

`A_3 =3^2\\\\A_3=9\;square\;unit`

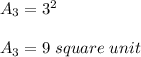
When n is 4, the area is given by;

`A_4=4^2\\\\A_4=16\;square\;unit`

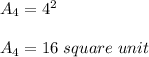
Part c.

The patterns in the areas indicates a recursive division of the total area into smaller, but similar equilateral triangles. The area of the seventh triangle in the pattern is given by;

`A_7=7^2\\\\A_7=49\;square\;unit`

In the pattern below, each small triangle is an equilateral triangle with an area of 1 square unit.

a. Explain how you know that any triangle made out of equilateral triangles will be an equilateral triangle.

b. Find the areas of the first four triangles in the pattern.

c. Describe any patterns in the areas. Predict the area of the seventh triangle in the pattern. Explain your reasoning.