Question

The food calorie, equal to 4186 j, is a measure of how much energy is released when the body metabolizes food. a certain fruit-and-cereal bar contains 140 food calories. if a 65-kg hiker eats one bar, how high a mountain must he climb to "work off" the calories, assuming all the food energy goes into increasing gravitational potential energy? (young, 7.4)

Answer 1

The hiker needs to climb approximately 694 meters to "work off" the calories from the fruit-and-cereal bar.

Step-by-step explanation:

To determine the height the hiker must climb to burn off the energy from the consumed bar, we can use the gravitational potential energy formula:
`\(PE = m * g * h\), where \(m\) is the mass (65 kg), \(g\)` is the acceleration due to gravity (9.8 m/s²), and (h) is the height.

First, convert food calories to joules using the given conversion: 1 food calorie = 4186 J. The bar contains 140 food calories, so its energy is
`\(140 \, \text{food calories} * 4186 \, \text{J/food calorie}\).`

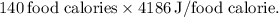
Then, equate this energy to the potential energy gained by the hiker. Rearrange the gravitational potential energy formula to solve for height:
`\(h = \frac{{\text{Energy}}}{{m * g}}\).`

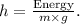
Substitute the values:
`\(h = \frac{{140 * 4186 \, \text{J}}}{{65 \, \text{kg} * 9.8 \, \text{m/s}^2}}\)` to find the height. After the calculation, the result is approximately 694 meters.

This calculation assumes all the food energy is converted solely into potential energy. In reality, the body utilizes energy for various metabolic processes, and not all consumed energy directly converts into potential energy. Additionally, individual metabolic rates and efficiency vary, so the actual height climbed to burn off the calories might differ for different individuals.