Final Answer:
a) According to the given least-squares regression equation, the predicted weight of a spotted bass that is 50 cm long is approximately 2.2 kg.
Step-by-step explanation:
The given least-squares regression equation is
 To find the predicted weight for a spotted bass of 50 cm length, we substitute
To find the predicted weight for a spotted bass of 50 cm length, we substitute
 into the equation.
into the equation.
![\[ \widehat{\log(\text{weight})} = 3.11 \cdot \log(50) - 4.94 \]](https://img.qammunity.org/2024/formulas/biology/high-school/koj1yz3b793o8zen69y7os8uhiutyk3ych.png)
Now, calculate the expression:
![\[ \widehat{\log(\text{weight})} = 3.11 \cdot 1.69897 - 4.94 \]](https://img.qammunity.org/2024/formulas/biology/high-school/2y18rqo2td99mycyevyaymjyzsaz1cf3gm.png)
![\[ \widehat{\log(\text{weight})} \approx 0.34257 \]](https://img.qammunity.org/2024/formulas/biology/high-school/7otp0ywpygzqpgzzuy7idr2s0jcovd6q36.png)
To find the predicted weight, we need to undo the logarithm transformation. So, we calculate
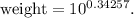
![\[ \text{weight} \approx 2.18 \, \text{kg} \]](https://img.qammunity.org/2024/formulas/biology/high-school/iz21hbmfz2u8esc4e1z5lu2va9mk9e0ltv.png)
Rounding to one decimal place, the predicted weight of a spotted bass that is 50 cm long is approximately 2.2 kg. The logarithmic transformation helps linearize the relationship between length and weight, making it easier to model and interpret. The regression equation provides a tool to estimate the weight of a spotted bass based on its length, allowing for more efficient and accurate biological studies.