Final Answer:
The area of the shaded region formed by a square with side length 16 units and a rectangle with dimensions 3 by 7 units is 155 square units.
Step-by-step explanation:
To calculate the area of the shaded region, we can find the individual areas of the square and the rectangle, then subtract the area of the rectangle from the area of the square.
The area
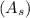 of the square is given by
of the square is given by
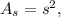 where
where
 is the side length. In this case,
is the side length. In this case,
 square units.
square units.
The area
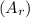 of the rectangle is given by
of the rectangle is given by
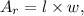 where
where
 is the length and
is the length and
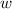 is the width. Here,
is the width. Here,

Therefore, the area of the shaded region
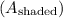 is obtained by subtracting the area of the rectangle from the area of the square:
is obtained by subtracting the area of the rectangle from the area of the square:
![\[ A_{\text{shaded}} = A_s - A_r = 256 - 21 = 155 \]](https://img.qammunity.org/2022/formulas/mathematics/college/2p3px93pqws0wllmge2wcpinot2s28f3vo.png) square units.
square units.
In conclusion, the area of the shaded region is 155 square units, demonstrating the application of basic geometric formulas for squares and rectangles.