Question

Find the formula for an exponential equation that passes through the points, (0,3) and (1,4). the exponential equation should be of the form

Answer 1

The formula for an exponential equation that passes through the points (0,3) and (1,4) is y = 3(4/3)^x.

Step-by-step explanation:

The formula for an exponential equation that passes through the points (0,3) and (1,4) can be found by plugging in the given points into the general form of an exponential equation: y = ab^x. Let's substitute the first point (0,3) into the equation:

3 = ab^0
3 = a(1)
a = 3

Now let's substitute the second point (1,4) into the equation:

4 = 3b^1
4 = 3b
b = 4/3

Therefore, the formula for the exponential equation that passes through the given points is y = 3(4/3)^x.

The complete question is: Find the formula for an exponential equation that passes through the points, (0,3) and (1,4). the exponential equation should be of the form is:

Answer 2

The exponential equation that passes through the points (0,3) and (1,4) and is in the form
`\(y = a \cdot b^x\)` is
`\(y = 3 \cdot 4^x\).`

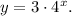
Step-by-step explanation:

To find the exponential equation, we use the general form
`\(y = a \cdot b^x\),` where
`\(a\)` is the initial value (the value of y) when
`\(x = 0\)),` and base is the base of the exponential function. Given the points (0,3) and (1,4), we can substitute these values into the equation.

First, when
`\(x = 0\), \(y = 3\).` This gives us the initial value
`\(a = 3\)`. Now, when
`\(x = 1\), \(y = 4\)`. Substituting these values into the equation, we get
`\(4 = 3 \cdot b^1\)`. Solving for b, we find b = 4. Therefore, the exponential equation is
`\(y = 3 \cdot 4^x\).`

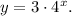
In this equation, the initial value of 3 represents the y-intercept, and the base of 4 determines the rate of growth. As
`\(x\)`increases by 1, the value of the function is multiplied by 4. This exponential growth is consistent with the given data points (0,3) and (1,4), making the equation
`\(y = 3 \cdot 4^x\)` the solution that satisfies the specified conditions.