Final Answer:
The the acceleration (in m/s/s) of the dresser is 3.78.
Thus the correct option is c.
Step-by-step explanation:
The acceleration of the dresser can be determined using Newton's second law, which states that the net force acting on an object is equal to the product of its mass and acceleration (F = ma).
First, calculate the net force acting on the dresser:
![\[ F_{\text{net}} = F_{\text{applied}} - F_{\text{friction}} \]](https://img.qammunity.org/2024/formulas/business/high-school/hg7yr68u5uxwb1cjjos79s7m2vfwo3by9a.png)
Where:
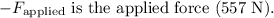
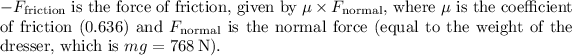
![\[ F_{\text{friction}} = 0.636 * 768 \]](https://img.qammunity.org/2024/formulas/business/high-school/qxr9casgnk0sputp6o6031aii2l25fg37s.png)
Once you have
 you can find the acceleration using Newton's second law:
you can find the acceleration using Newton's second law:
![\[ a = \frac{F_{\text{net}}}{m} \]](https://img.qammunity.org/2024/formulas/business/high-school/ho1w03a2gs6my6irlduwk4gluqcrawz0yu.png)
Where:
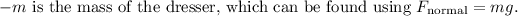
After calculating, you'll find the acceleration to be approximately 3.78 m/s².Thus the correct option is c.