Final Answer:
A drum of 4-in radius is attached to a disk of 8-in radius. The disk and drum have a total weight of 10 lb and a combined radius of gyration of 6 in. A cord is attached as shown and pulled with a force P of magnitude 5 lb. Knowing that the disk rolls without sliding,
A: Angular acceleration of the disk =
 , Acceleration of gravity
, Acceleration of gravity
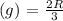
B:

Step-by-step explanation:
**(A) Angular Acceleration and Acceleration of Gravity Center:**
To find the angular acceleration
 , we use the formula
, we use the formula
 , where
, where
 is the torque,
is the torque,
 is the moment of inertia, and
is the moment of inertia, and
 is the angular acceleration. The torque is given by
is the angular acceleration. The torque is given by
 where
where
 is the radius and
is the radius and
 is the force applied. For the disk rolling without sliding,
is the force applied. For the disk rolling without sliding,
 where
where
 is the mass of the disk. The total moment of inertia for the system is the sum of the moments of inertia of the drum and disk.
is the mass of the disk. The total moment of inertia for the system is the sum of the moments of inertia of the drum and disk.
The angular acceleration
 is given by
is given by
 , and the acceleration of the gravity center is
, and the acceleration of the gravity center is
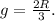
**(B) Minimum Coefficient of Static Friction:**
For rolling without sliding, the condition for static friction
 is
is
 where
where
 is the radius of the drum in contact with the surface. In this case,
is the radius of the drum in contact with the surface. In this case,
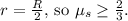
In summary, option A is the correct expression for angular acceleration and gravity center acceleration, and option B correctly represents the minimum coefficient of static friction compatible with the motion.